Processing data
Fitting SSM’s to tracking data in aniMotum is intended
to be as simple as possible using fit_ssm(). Provided the
data are in an expected format (see vignette('Overview')),
fit_ssm can be invoked immediately to both process the data
and fit the SSM. Within fit_ssm, data processing consists
of:
- identifying the most appropriate measurement error model to use
based on the format of the data;
- date formatting, ordering observations in time, flagging duplicate
date-time observations, flagging observations occurring within a minimum
time period (default = 60 s);
- projecting long,lat coordinates to Mercator x,y (in km) accounting
for -180,180 crossing;
- using
trip::sdato identify potentially extreme observations based on speed, distance, and angle (Freitas et al. 2008).
Several arguments to fit_ssm provide a measure of
control over data processing. The vmax, ang
and distlim arguments provide control over the
trip::sda filter (see ?fit_ssm for details).
The sda filter can occasionally fail (possibly when
calculating angles between successive displacements), in this case we
fall back to using trip::speedfilter and a warning issued.
The trip filter can be turned off altogether with
spdf = FALSE, although this is usually not advisable if
working with older Least-Squares Argos data, the lower prevalence of
extreme observations in newer Kalman filtered Argos data may not always
require speed-filtering prior to fitting an SSM. The minimum time
interval allowed between observations is set by min.dt.
Finally, the processed data can be returned, e.g. for careful
inspection, without fitting an SSM with the pf = TRUE
argument:
fit_ssm(ellie,
vmax = 3,
pf = TRUE)By setting pf = TRUE, fit_ssm returns the
processed data as a projected sf data.frame prior to
fitting an SSM. Looking at the keep column, we can see that
the 3rd, 4th and 7th observations have been flagged to be ignored by the
SSM, in this case because they failed the distance limits imposed by the
trip::sda filter. Also note that because the data included
CLS Argos location ellipse error information, the observation type has
been designated KF for Kalman filter and this ensures that
the appropriate measurement error model is used when fitting the SSM to
these data.
Fit an SSM
In the simplest case, fitting an SSM consists of specifying the process model and a prediction time step:
fit <- fit_ssm(ellie,
model = "rw",
time.step = 24)This call uses the defaults for data processing and all other
arguments (see ?fit_ssm for details). More control can be
exerted over the model fitting process via the arguments:
emf, map, and control.
emf: specifying error multiplication factors
The emf argument is helpful when modelling older Argos
Least-Squares location data as it allows alternate specification of
error multiplication factors for each location quality class. The error
multiplication factors define the magnitude of the location error
standard deviation for each Argos location quality class relative to the
best quality class, 3. The emf’s used by default in
aniMotum (see Jonsen et al. 2020 for further details) are
unlikely to be equally applicable to all tracking data sets. Alternate
specifications could be derived from Argos location error studies that
draw on Argos - GPS double-tagging data such as (Costa et al. 2010).
The default emf values are given by emf():
emf()
#> emf.x emf.y lc
#> 1 0.10 0.10 G
#> 2 1.00 1.00 3
#> 3 1.54 1.29 2
#> 4 3.72 2.55 1
#> 5 13.51 14.99 0
#> 6 23.90 22.00 A
#> 7 44.22 32.53 B
#> 8 44.22 32.53 ZThese can be adjusted by modifying the data.frame and passing this to
fit_ssm via `emf.
emf2 <- dplyr::mutate(emf(), emf.x = c(0.1, 1, 2, 4, 20, 8, 15, 15))
fit1 <- fit_ssm(subset(sese2, id == unique(id)[1]),
model = "rw",
time.step=24,
control = ssm_control(verbose = 0))
fit2 <- fit_ssm(subset(sese2, id == unique(id)[1]),
model = "rw",
time.step=24,
emf = emf2,
control = ssm_control(verbose = 0))
par(mfrow = c(2,1), mar = c(4,3,1,1))
hist(grab(fit1, "f")$x - grab(fit2, "f")$x, breaks = 20,
main = "fit1$x - fit2$x", xlim = c(-20,20), xlab = "")
hist(grab(fit1, "f")$y - grab(fit2, "f")$y, breaks = 20,
main = "fit1$y - fit2$y", xlim = c(-20,20), xlab = "Distance (km)")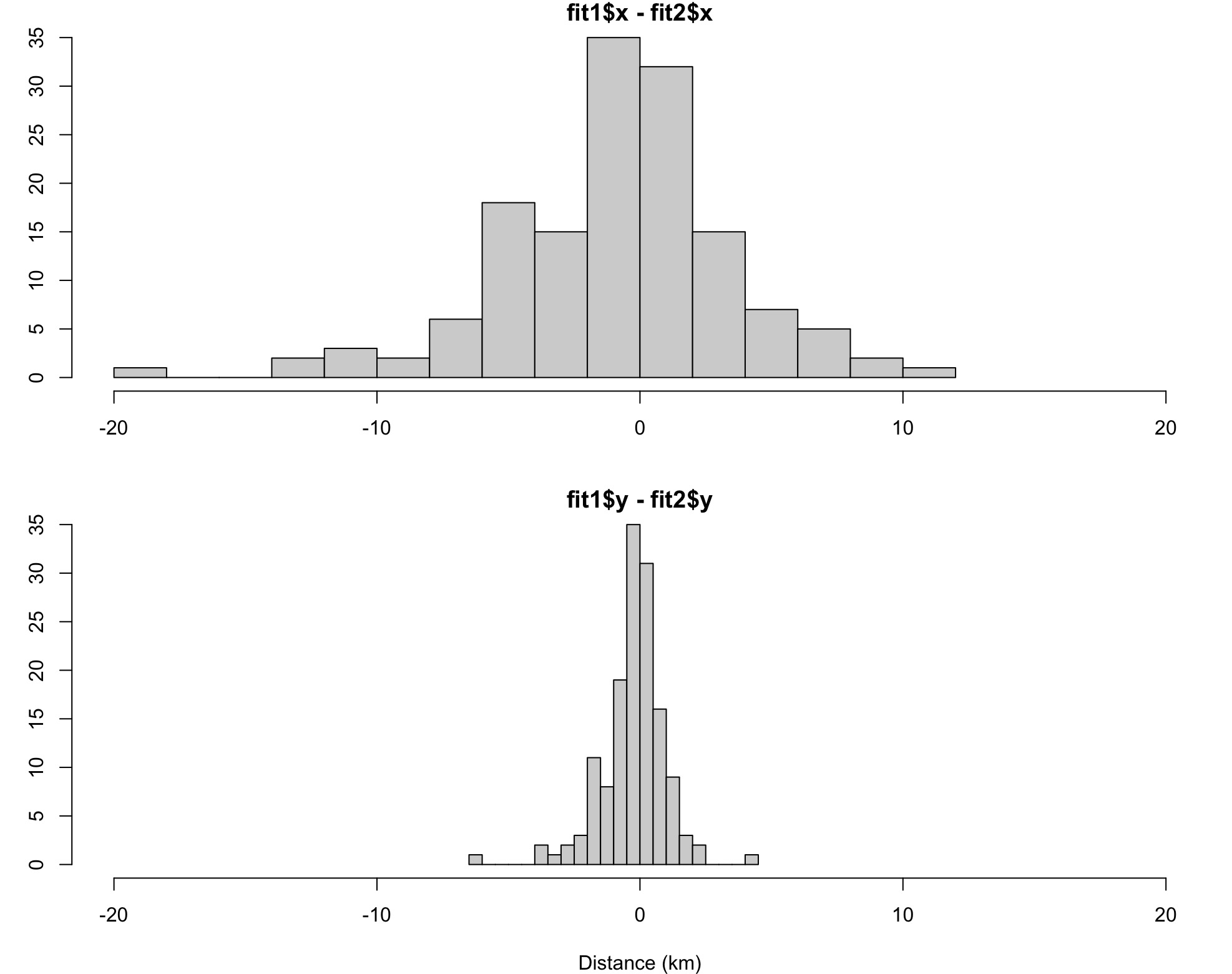
In this contrived example, re-specified emf.x values
result in differences in the predicted locations of up to about 20 km in
the x-direction and a more subtle 4 km in the y-direction, even though
the emf.y values were not edited. The latter is due to a
model-estimated correlation between the x and y errors.
Now that CLS Argos provides locations estimated by their Kalman
filter algorithm, users of contemporary Argos data sets should have no
need to invoke the emf argument as location quality
class-based errors are now superseded by the use of location-specific
Argos error ellipse information (McClintock et al. 2015; Jonsen et
al. 2020).
map: fixing model parameters
The map argument allows some model parameters to by
turned off by fixing them at 0 on the log-scale. This can be useful in
cases where model simplification can aid in convergence or simply
provide a better fit to the data. For example, the crw has
a parameter psi that re-scales the semi-major axis of Argos
KF error ellipses to account for apparent bias in the error ellipses
(Jonsen et al. 2020). Occasionally, there may be insufficient
information to reliably estimate this parameter, or one might wish to
compare model fits with and without error ellipse bias correction.
Here we fit the crw model with (fit1) and
without (fit2) the bias-correction parameter
psi, by supplying a named list to the map
argument. Where factor(NA) is a TMB convention
that ensures psi is fixed during optimization.
fit1 <- fit_ssm(ellie,
model = "crw",
time.step = 24,
control = ssm_control(verbose = 0))
fit2 <- fit_ssm(ellie,
model = "crw",
time.step = 24,
map = list(psi = factor(NA)),
control = ssm_control(verbose = 0))
c(fit1$ssm[[1]]$AICc, fit2$ssm[[1]]$AICc)#> [1] 1292.494 1295.789Comparison of AICc from the model fits implies the model
including the psi parameter fit1 provides a
slightly better fit.
control: controlling the optimization
By default, aniMotum uses R’s nlminb
optimizer, but users can also select the more flexible
optim to minimize the objective function defined by the
built-in TMB C++ templates. Users can specify which
optimizer to use via the control argument, which takes a
named list as input that is provided by the utility function
`ssm_control:
fit <- fit_ssm(ellie,
model = "crw",
time.step = 24,
control = ssm_control(optim = "optim",
verbose = 0))Here, we use control = ssm_control() to set the
optimizer to optim and turned off the parameter trace that
would be printed to the console by default. See
?ssm_control for further options. Both of optimizers rely
on a list of control parameters that allow fine-tuning of the
optimization process, which can aid convergence on tricky data sets.
Users can specify any of these control parameters in
ssm_control, for example:
fit <- fit_ssm(ellie,
model = "crw",
time.step = 24,
control = ssm_control(optim = "optim",
maxit = 1000,
verbose = 0))Here we increase the maximum number of optimizer iterations from 100
(optim default for derivative-based methods) to 1000. Note,
users must know the correct name for each optimizer’s control arguments
and should be familiar with their effect on the optimization before
using, see ?nlminb and ?optim for details.
The control argument is used to turn off parameter trace
printing via ssm_control(verbose = 0) in all above
examples. This keeps the vignette tidy as the default parameter trace
would print as a long list to the vignette. In normal use in the
console, the parameter trace overwrites itself on a single line per
individual data set and is provided as a guide to model fitting
progress. The full inner and outer optimization as reported by
TMB (Kristensen et al. 2016) can also be printed to the
console by setting ssm_control(verbose = 2); this can be
helpful in diagnosing convergence failures or optimization errors.
Finally, the ssm_control(se = TRUE) argument can be
invoked when fitting the crw SSM to turn on computation of
SE’s for speed-along-track estimates. By default, these SE’s are turned
off as their calculation require considerable computation, which
increases with the number of prediction intervals, and dramatically
increases the time required to fit the crw model.
References
Costa DP, Robinson PW, Arnould JPY, Harrison AL, Simmons SE, Hassrick JL, Hoskins AJ, Kirkman SP, Oosthuizen H, Villegas-Amtmann S, Crocker DE (2010) Accuracy of ARGOS locations of pinnipeds at-sea estimated using Fastloc GPS. PLOS One 5:e8677.
Freitas C, Lydersen C, Fedak MA, Kovacs KM (2008) A simple new algorithm to filter marine mammal Argos locations. Marine Mammal Science 24: 315-325.
Jonsen ID, Patterson TA, Costa DP, Doherty PD, Godley BJ, Grecian WJ, Guinet C, Hoenner X, Kienle SS, Robinson PW, Votier SC, Whiting S, Witt MJ, Hindell MA, Harcourt RG, McMahon CR (2020) A continuous-time state-space model for rapid quality control of Argos locations from animal-borne tags. Movement Ecology 8:31.
Kristense K, Nielsen A, Berg CW, Skaug H, Bell BM (2016) TMB: automatic differentiation and Laplace approximation. Journal of Statistical Software 70:1-21.
McClintock BT, London JM, Cameron MF, Boveng PL (2015) Modelling animal movement using the Argos satellite telemetry location error ellipse. Methods in Ecology and Evolution 6:266–77.