Track_simulation

Source: vignettes/Track_simulation.Rmd

aniMotum provides 2 track simulation functions for simulating random tracks from a few different movement process models, sim(), and for simulating random tracks from fitted SSM models, sim_fit().

sim()

The sim function is useful for situations where simulated random tracks are required, such as understanding how observed animal tracks deviate from the expectations of the rw, crw or mp movement process models, or for exploring potential bias in SSM fits to data. Tracks can be simulated with regular or random time intervals between locations via the tdist, ts and tpar arguments, and with Argos Least-Squares- or Kalman filter-based location errors via the error, tau and rho_o arguments. Multiple behavioural states with stochastic switching can be implemented for the rw and crw models via the alpha argument.

Simulate tracks from each of the 3 process models 

set.seed(pi) 
sim.rw <- sim(N = 200, model = "rw")
sim.crw <- sim(N = 200, model = "crw", D = 0.5)
sim.mp <- sim(N = 200, model = "mp", sigma_g = 0.3)

Plot simulated tracks 

(plot(sim.rw, type=2) + labs(title="'rw'") | plot(sim.crw, type=2) + labs(title="'crw'")) / 
  (plot(sim.mp, type = 2) + labs(title="'mp'") | plot(sim.mp, type = 1)) + 
  plot_layout(guides = 'collect') & 
  theme(legend.position = 'bottom')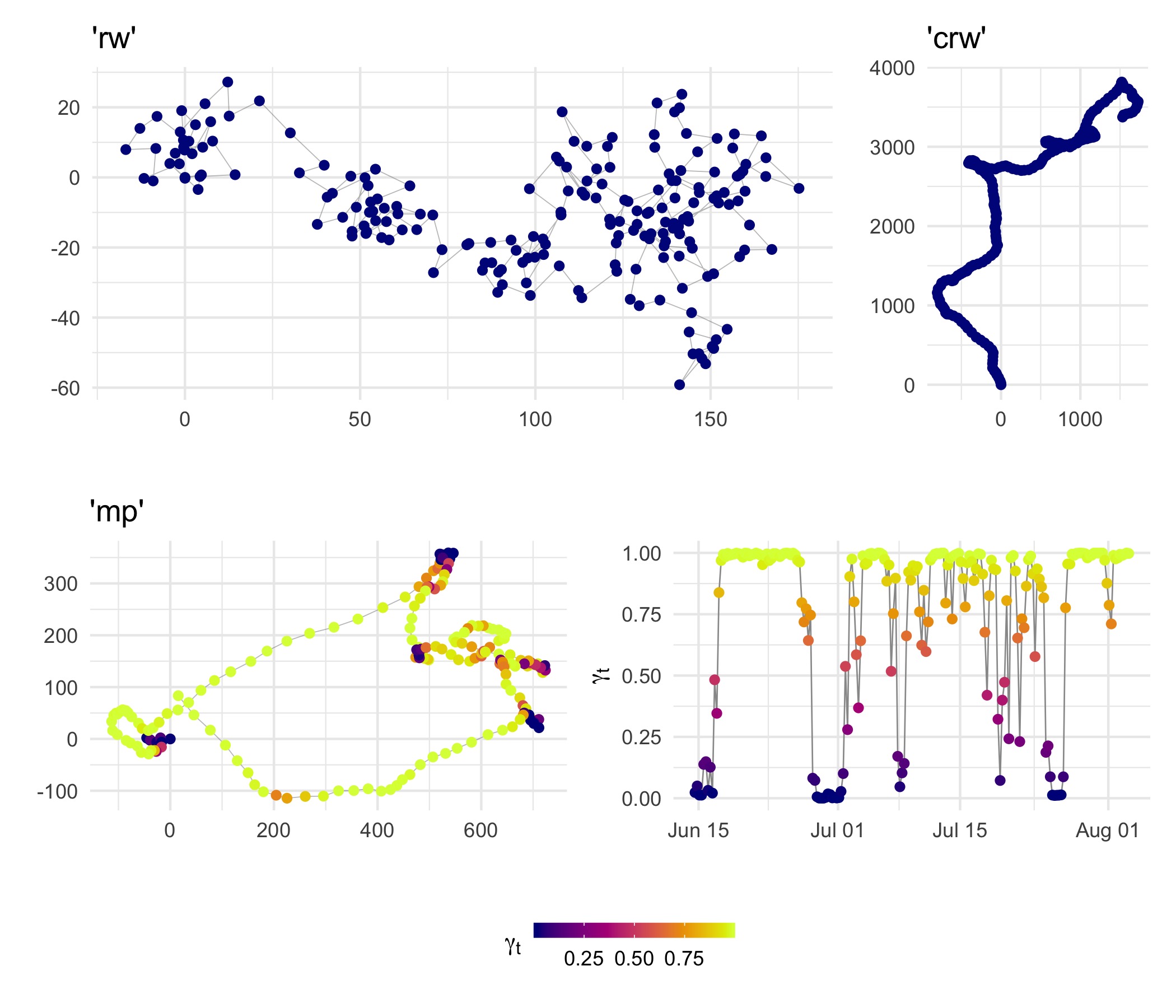

Fit SSM to simulated lon,lat locations (with Argos error) 

# coerce simulated RW data to format expected by fit_ssm
d <- with(sim.rw, data.frame(id = 1, date, lc, lon, lat))

# fit SSM `rw` model without any speed filtering
fit.rw <- fit_ssm(d, 
                  spdf = FALSE, 
                  model = "rw", 
                  time.step = 12, 
                  control = ssm_control(verbose = 0))

# fit SSM `crw` model
fit.crw <- fit_ssm(d, 
                   spdf = FALSE, 
                   model = "crw", 
                   time.step = 12, 
                   control = ssm_control(verbose = 0))

# extract SSM fitted locations
loc.rw <- grab(fit.rw, "fitted")
loc.crw <- grab(fit.crw, "fitted")
# compare estimated to true values in y-direction
ggplot() +
  geom_point(data = sim.rw, aes(date, I(y+y.err)), col = "grey60") +       # y-values observed with Argos error
  geom_point(data = sim.rw, aes(date, y), col = "dodgerblue") +            # true y-values
  geom_point(data = loc.rw, aes(date, y), cex = 0.7, col = "firebrick") +  # RW SSM fitted y
  geom_point(data = loc.crw, aes(date, y), cex = 0.4, col = "orange")      # CRW SSM fitted y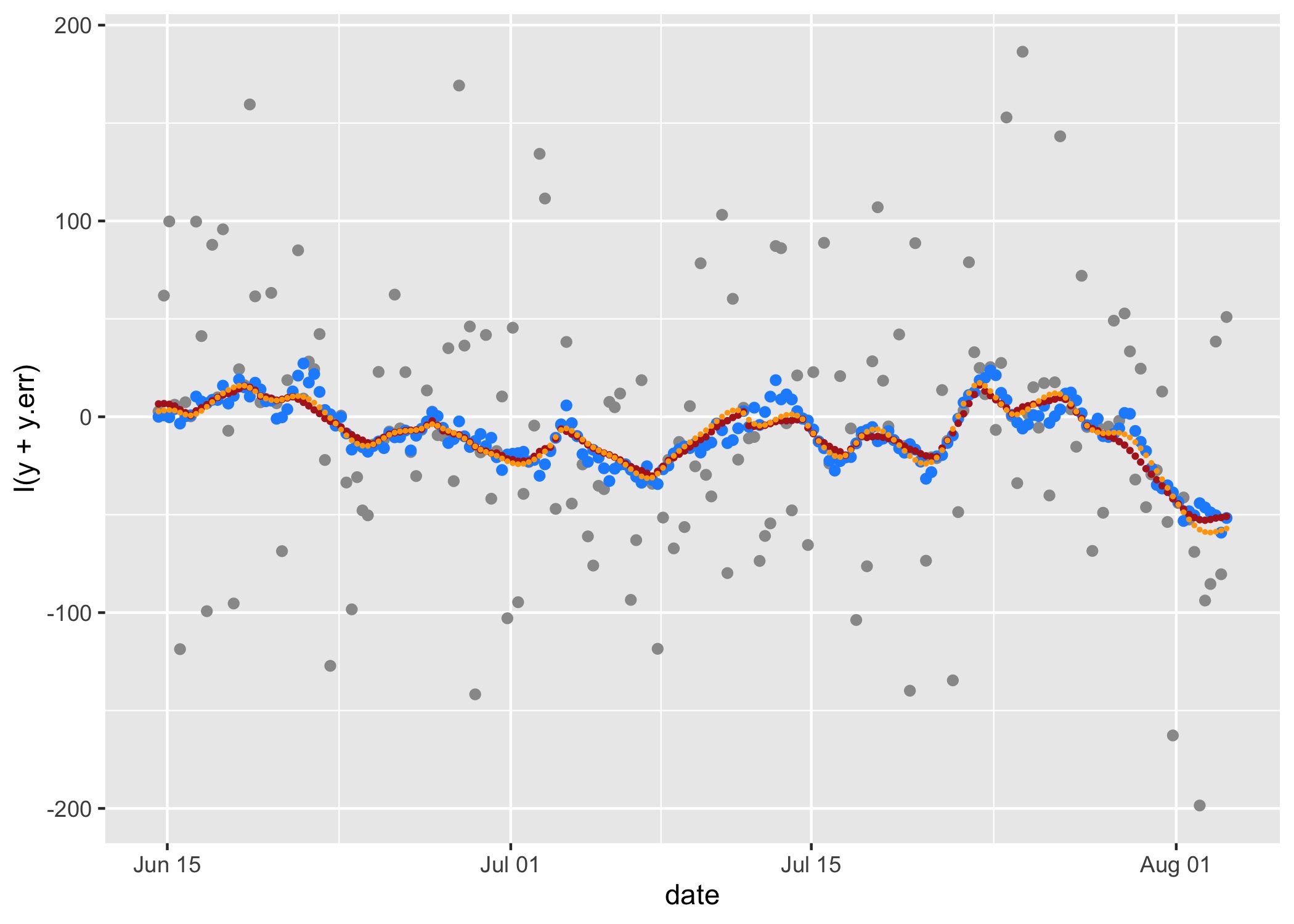

The rw (red) and crw (orange) SSM’s yield similar, reasonable fits to the RW simulated track, although both tend to smooth through some of the natural variability in the simulated true y-values (blue). This reflects a common inability of SSM’s to fully separate process and measurement variability in an unbiased manner, especially when measurement error is greater than natural variability (Auger-Méthé et al. 2016).

sim_fit()

The sim_fit function is rather different, taking a aniMotum SSM fit object (class ssm_df) and simulating replicate tracks by using the movement parameter estimates from the fitted model. Currently, tracks can be simulated from rw and crw SSM model fits. Tracks can be simulated from either the observation times (what = "fitted") or the prediction times (what = "predicted") and, thus, are constrained to have the same number of locations. The simulated tracks are otherwise unconstrained and should not be considered as resampled tracks suitable for exploring uncertainty in the SSM-estimated track. They are useful for habitat usage modelling, to represent habitat that is potentially available to a collection of tracked individuals (e.g., Hindell et al. 2020).

Simulate tracks from an SSM fit and plot: 

set.seed(pi)
fit <- fit_ssm(sese2, 
               model="crw", 
               time.step=24, 
               control=ssm_control(verbose=0))

st <- sim_fit(fit[2,], what="predicted", reps=5)

plot(st)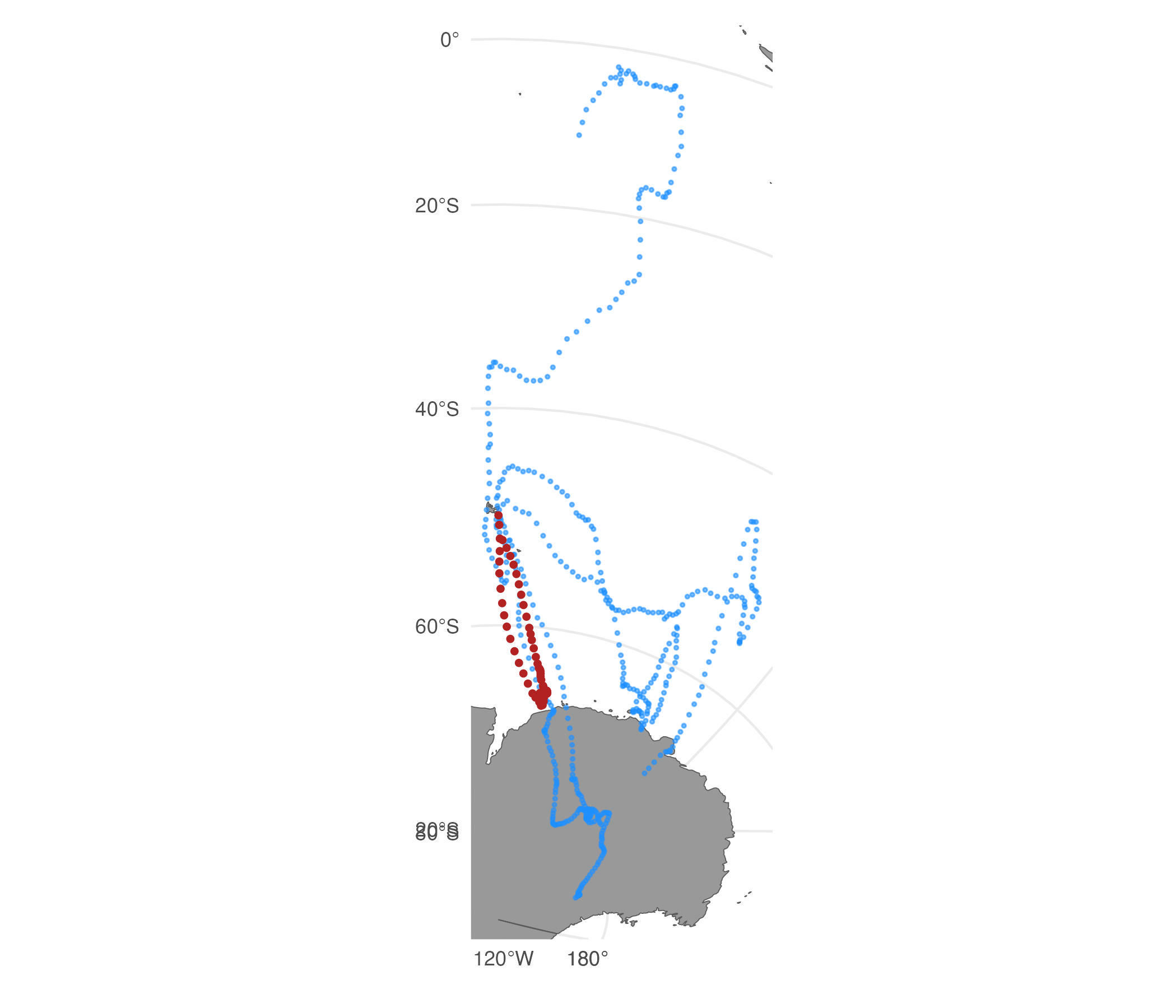

In this case, 3 of the 5 replicate tracks cross onto the Antarctic continent. We can further constrain the tracks to avoid land by adding a potential function (Brillinger et al. 2012) to the simulation that down-weights movements that cross onto land.

Simulate tracks with a potential function to help avoid land: 

load(system.file("extdata/grad.rda", package = "aniMotum"))
grad <- terra::unwrap(grad)

set.seed(pi)
st.pf <- sim_fit(fit[2, ], what = "predicted", reps=5, grad=grad, beta=c(-300,-300))

plot(st.pf)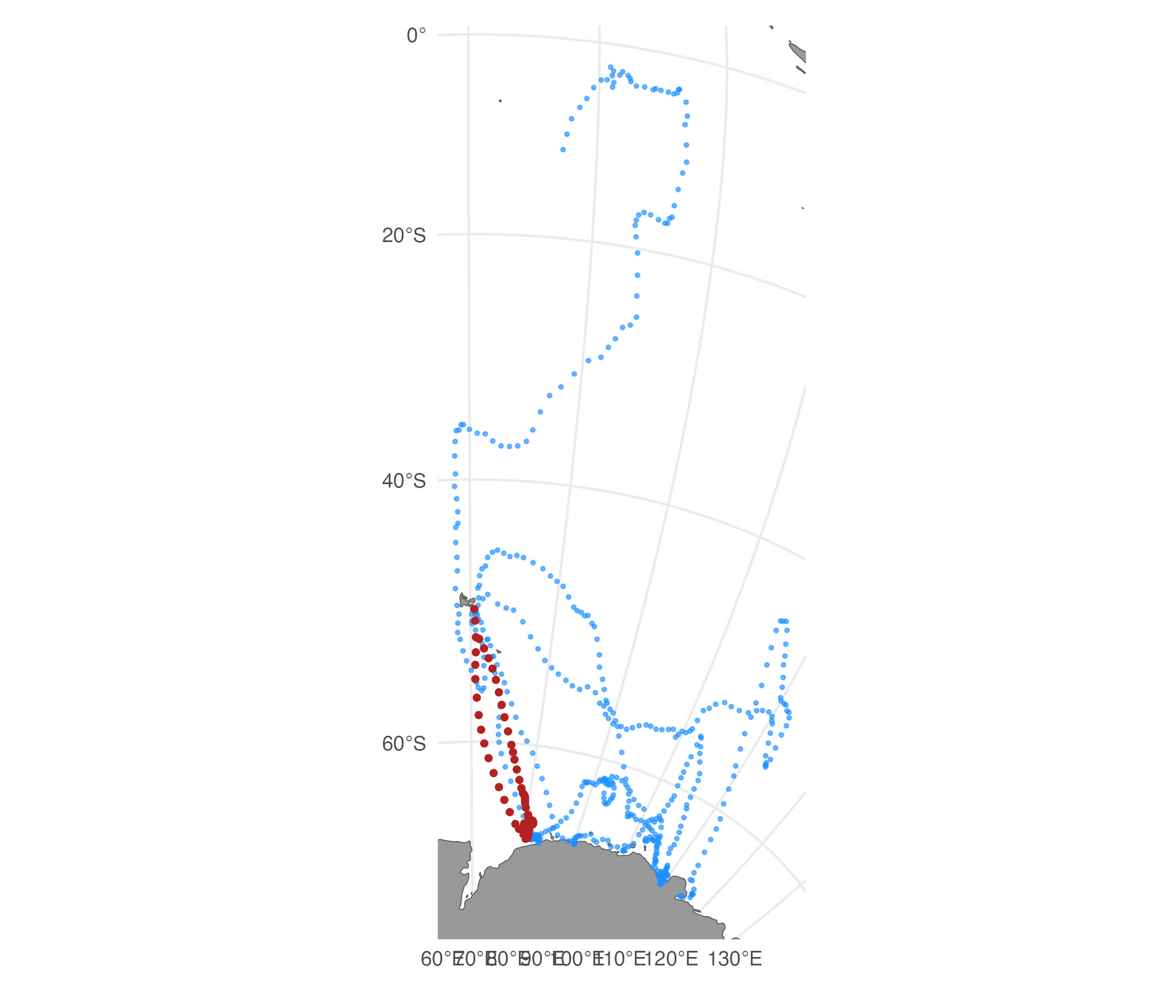

Here, we use built in gradient rasters based on distance from ocean and strongly negative beta parameters (for the x and y directions, respectively) to repel movements onto land. Custom gradients can be supplied, e.g., for finer-scale tracks or for other kinds of barriers to movement. The strength of the potential function can be varied by altering the magnitude of the beta parameters (but they must always be negative to avoid land). Note that with beta = c(-300,-300), the tracks do not all entirely avoid land. Features such as narrow islands or peninsulas pose a particular difficulty for this method, and tracks are not always guaranteed to remain off land. Adjustment of the beta values can yield a stronger (more negative) or weaker (less negative) repulsion from land, however the stronger the repulsion the more likely that unrealistic artefacts (e.g., zig-zagging movements) are introduced in the simulated tracks.

Simulate central place foraging tracks

The SSM-estimated track in the above example implies a central place foraging strategy, where the southern elephant seal departs from its breeding colony on Iles Kerguelen for an extended period of time and eventually returns. The simulated tracks do not reflect this strategy because the crw SSM fitted to the data does not have long-term memory or any other mechanism that could mimic the return portion of the foraging trip. We can, however, constrain the simulated tracks to return to their origin by applying a simple Brownian Bridge using the cpf argument:

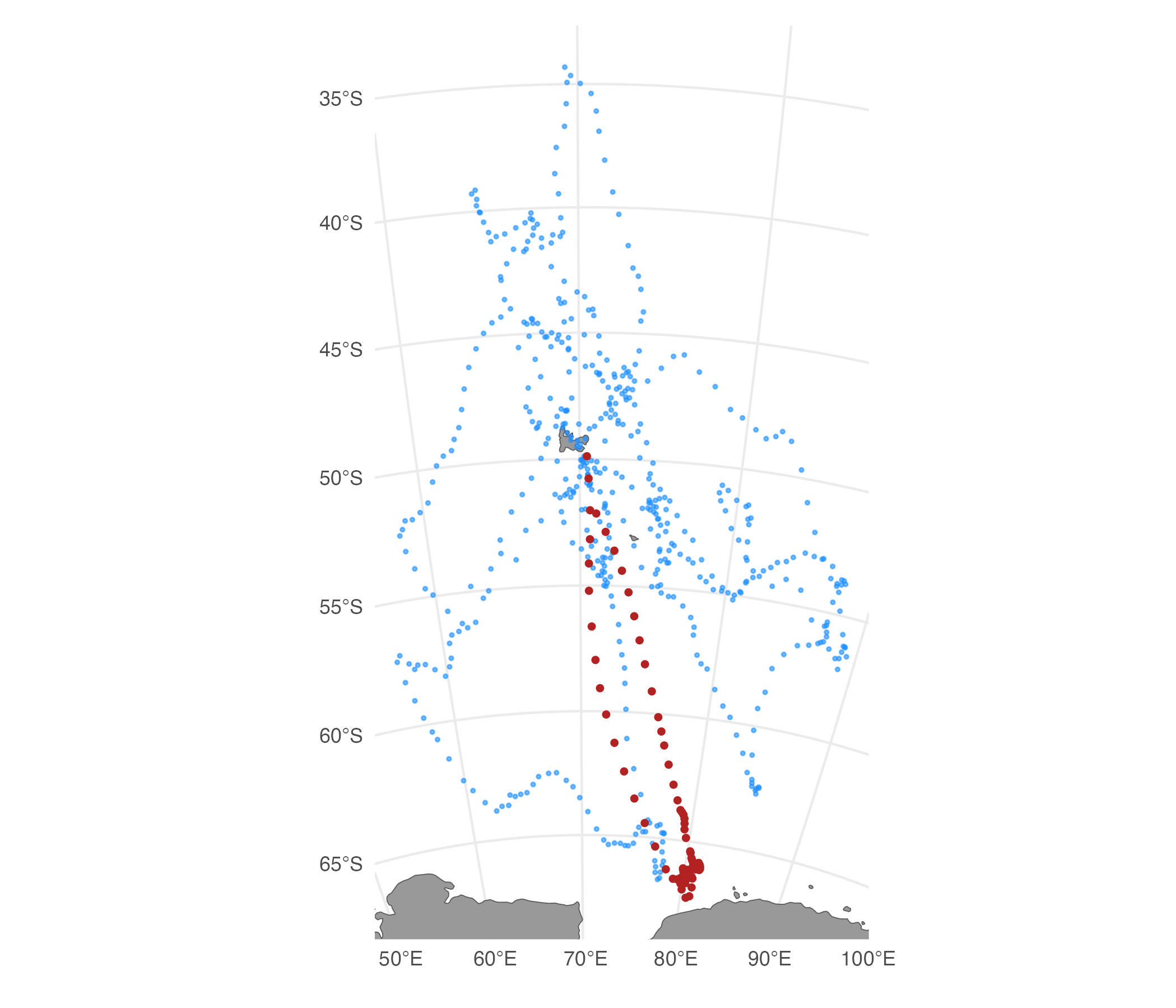
st.cpf <- sim_fit(fit[2, ], what = "predicted", reps=5, cpf = TRUE)

plot(st.cpf)

The cpf argument can be used in conjunction with the potential function, however, care should be taken as their implementations are independent with the potential function applied first. This means tracks that successfully avoid crossing land due to the potential function are not guaranteed to remain so after applying the cpf argument.

sim_filter()

When simulating a large number of replicate tracks using sim_fit, some portion of the simulations may reflect unrealistic movement patterns due to the relatively unconstrained nature of the simulation. A simple approach for identifying and removing less realistic simulated tracks is to use a similarity filter (e.g., Hazen et al. 2017). The sim_filter function can calculate two related similarity functions, based on a comparison of the geodesic distances and bearings from the start and end locations of the SSM fitted track and each of the simulated tracks. Simulated tracks can be discarded by defining a threshold quantile via the keep argument.

# simulate 50 tracks
st <- sim_fit(fit[1,], what = "predicted", reps = 50)

# filter, keep only top 20 %
st_f <- sim_filter(st, keep = 0.2)

# compare unfiltered vs. filtered tracks
plot(st) | plot(st_f)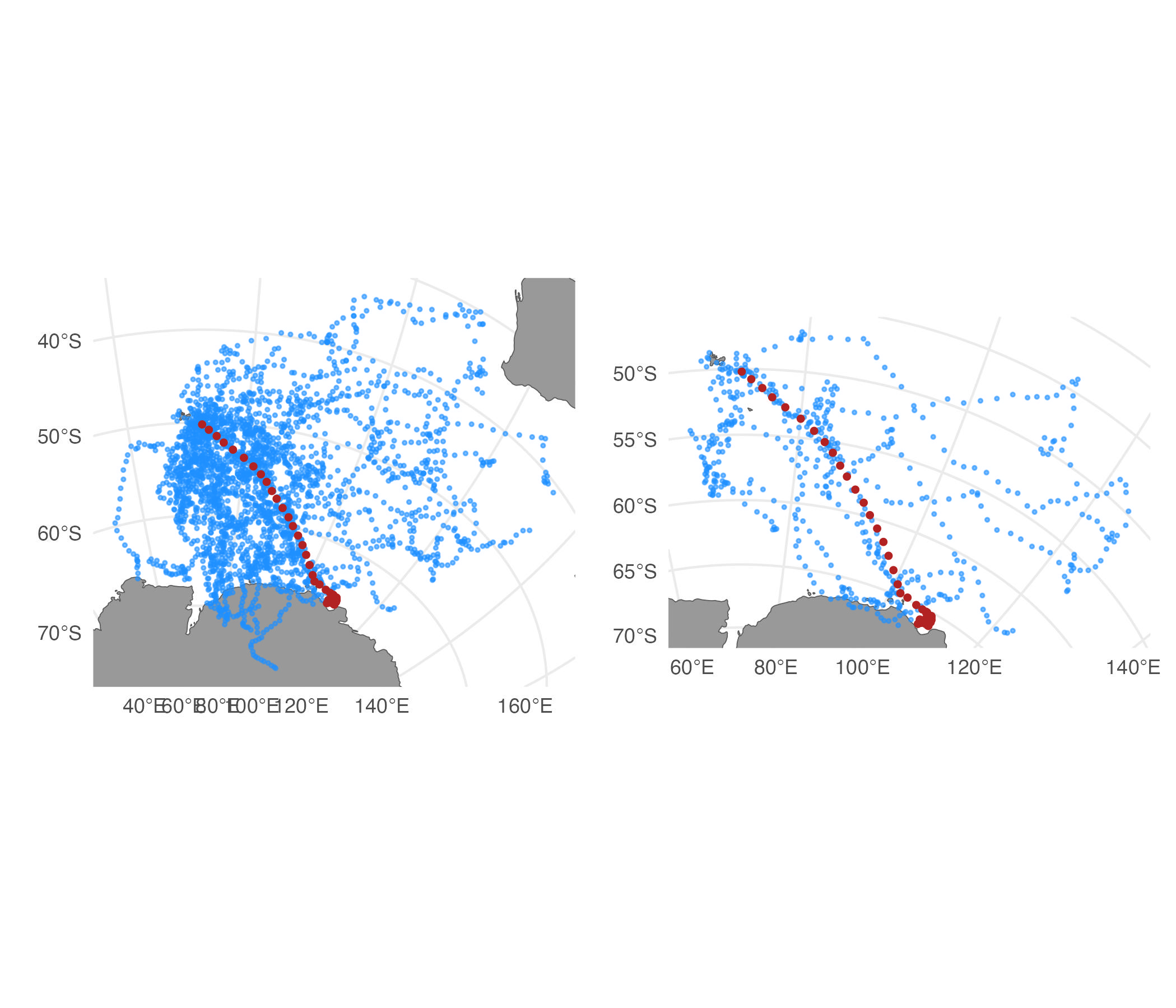

sim_filter handles central place foraging tracks automatically by comparing distances and bearings from the start location to the most distant location.

# simulate 50 cpf tracks
st.cpf <- sim_fit(fit[2,], what = "predicted", reps = 50, cpf = TRUE)

# filter, keep only top 20 %
st.cpf_f <- sim_filter(st.cpf, keep = 0.2)

# compare unfiltered vs. filtered tracks
plot(st.cpf) | plot(st.cpf_f)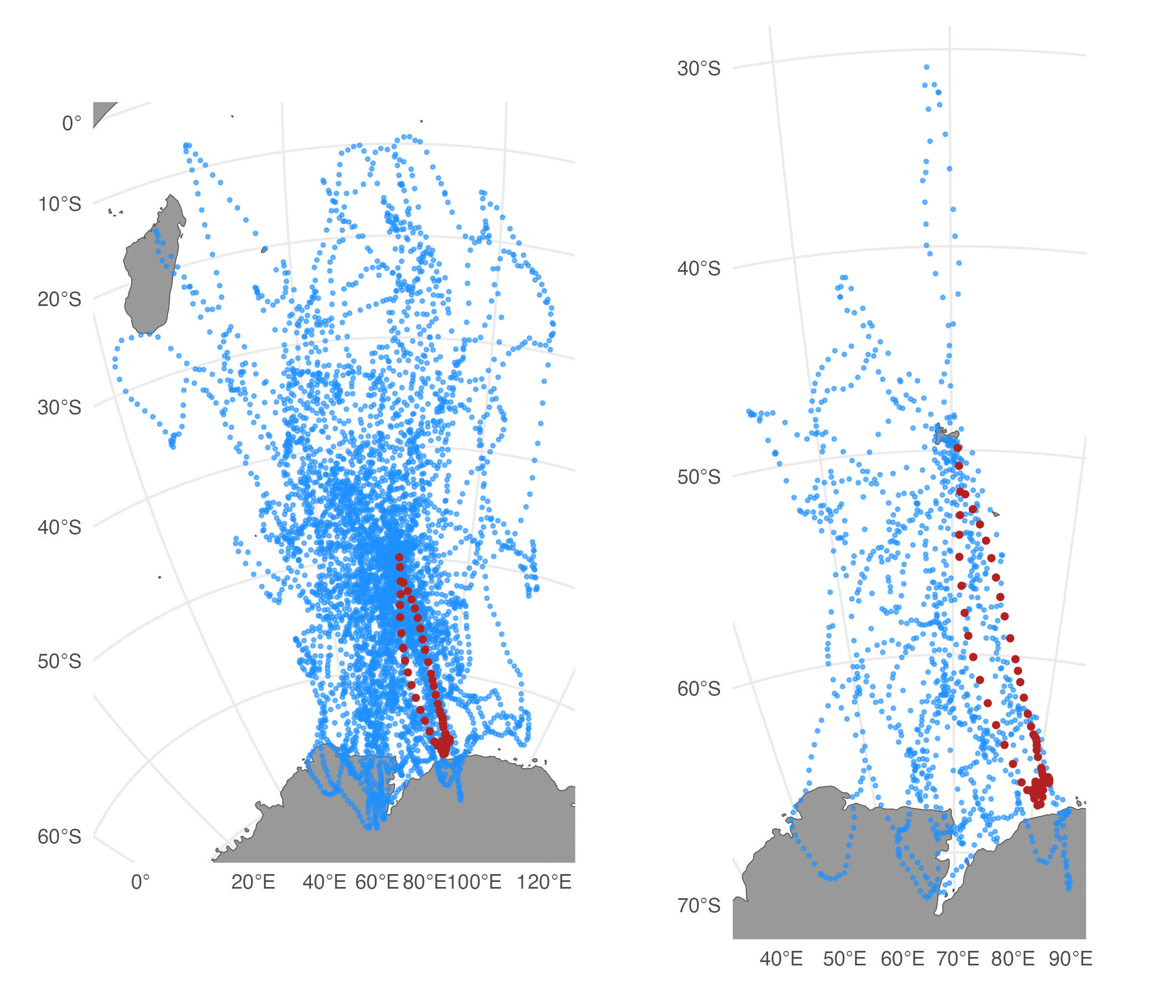

Alternatively, we can filter tracks based on a comparison of the summary statistics of arbitrary variables. For example, we could filter based on a comparison of the mean longitude and latitude of the SSM fitted versus simulated tracks.


st.cpf_f1 <- sim_filter(st.cpf, keep = 0.2, var = c("lon","lat"), FUN = "mean")

# compare tracks filtered by similarity flag vs mean lon,lat
plot(st.cpf_f) | plot(st.cpf_f1)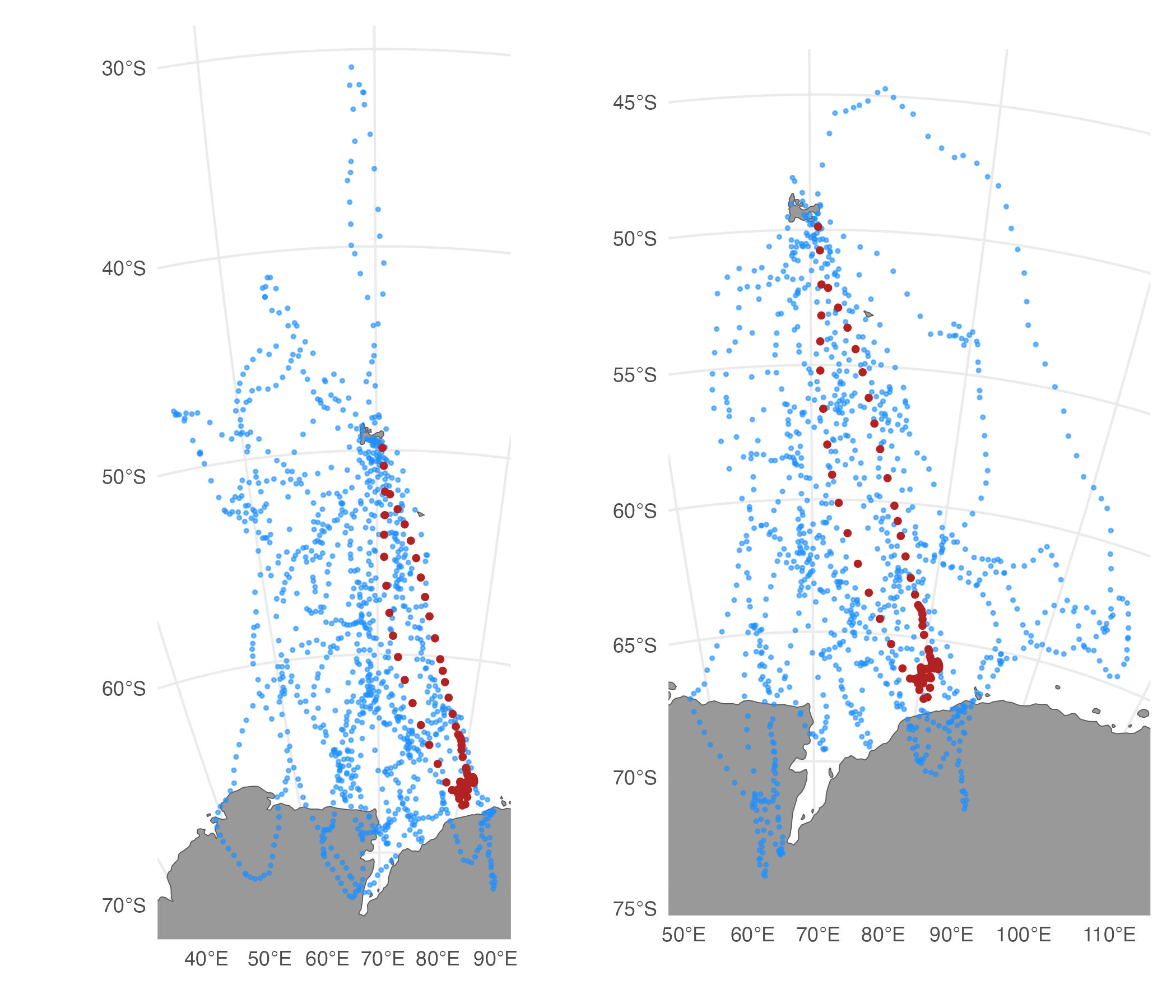

We can also filter tracks based on a new variable appended to the tracks. Here we use a raster of chlorophyll a values. We extract those values at each track location using the terra package and append them to the simulated track object.

chl <- terra::rast("../data-raw/chl.grd")

st.cpf.df <- tidyr::unnest(st.cpf, cols = c(sims))

## extract chl values at track locations
st.cpf.df <- st.cpf.df |> 
  dplyr::mutate(terra::extract(chl, cbind(lon, lat))) |>
  dplyr::rename(chl = chl_summer_climatology)

## convert back to nested tibble
st.cpf.n <- tidyr::nest(st.cpf.df, sims = c(rep, date, lon, lat, x, y, chl))

## append new nested tibble with correct aniMotum classes so sim_filter works
class(st.cpf.n) <- append(class(st.cpf)[1:2], class(st.cpf.n))

## filter based on mean chl values
st.cpf.chl <- sim_filter(st.cpf.n, keep = 0.2, var = "chl", FUN = "mean", na.rm = TRUE)

## plot filtered tracks
plot(st.cpf.chl)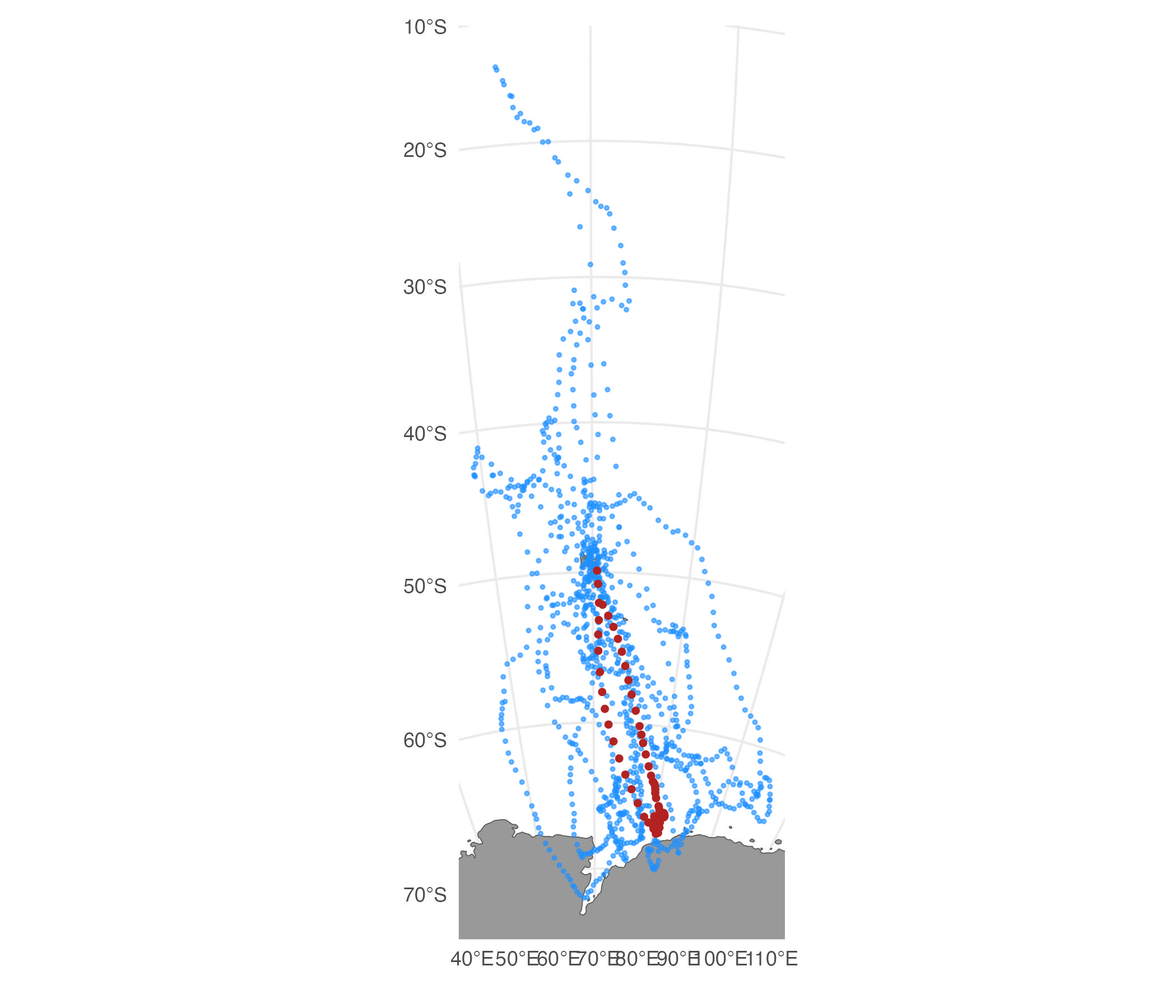

route_path()

We can use route_path() (see vignette('Path_rerouting') for more details) to re-route the few simulated track segments that cross land.

# reroute simulated tracks
st.cpf_f1rr <- route_path(st.cpf_f1, centroids = TRUE)

# compare
plot(st.cpf_f1) | plot(st.cpf_f1rr)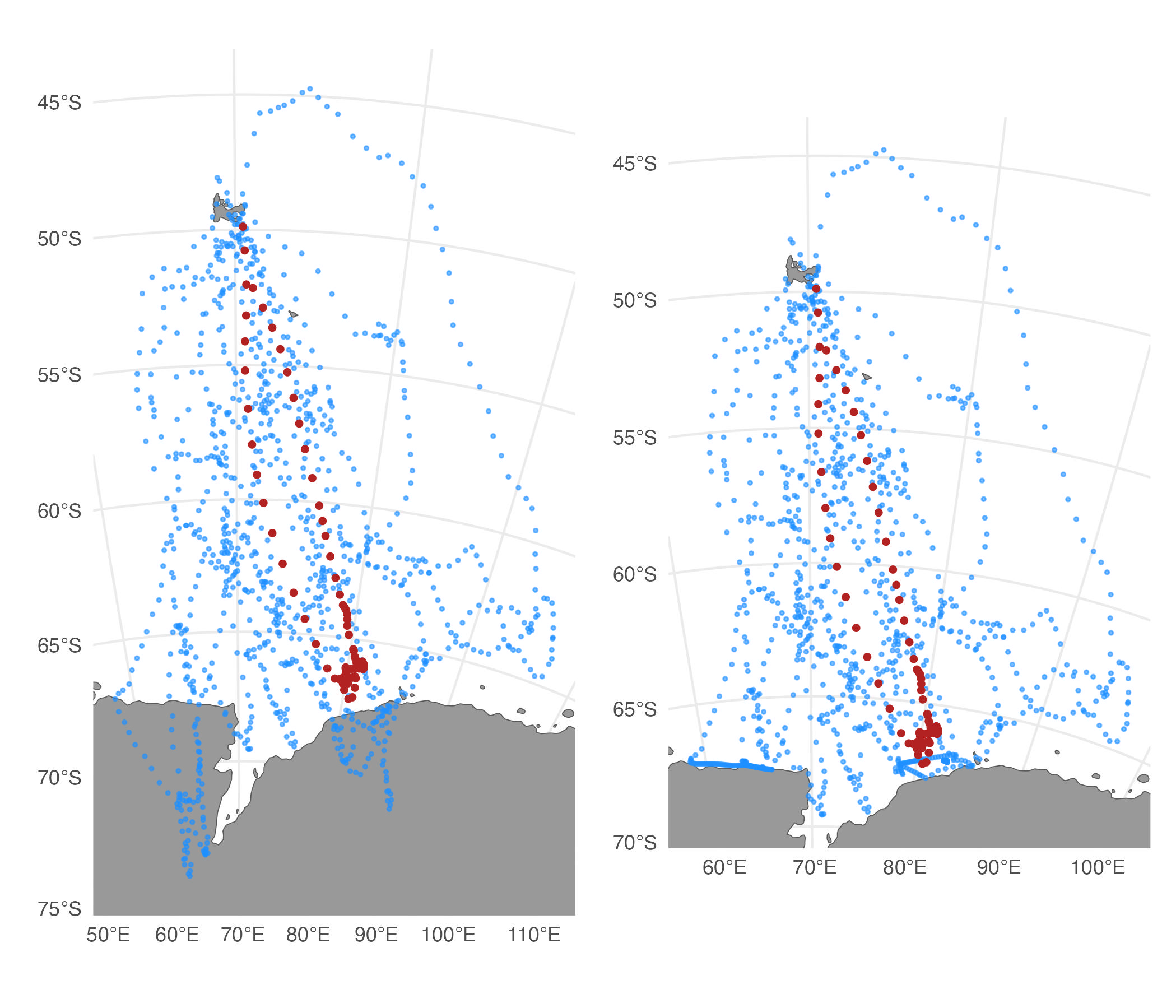

In more severe cases, tracks first could be simulated using potential functions, filtered, and then any remaining segments re-routed from land.

Simulate tracks from the posterior of SSM fit(s) - sim_post()

Posterior simulations from an SSM fit provide a useful characterization of track uncertainty. The sim_post function provides an efficient method for simulating tracks from the joint uncertainty of the estimated locations. These simulated tracks can be visualised using plot() (see ?plot.sim_post for details), or they can be extracted and used in subsequent analyses where multiple imputation is desired. A future version will include the option to incorporate uncertainty in the SSM movement parameters.

fit <- fit_ssm(sese2, model = "rw", time.step=6, control = ssm_control(verbose = 0))
psim <- sim_post(fit[2,], what = "predicted", reps = 100)

plot(psim, type = "lines", alpha = 0.05) | plot(psim, type = "both", alpha = 0.05)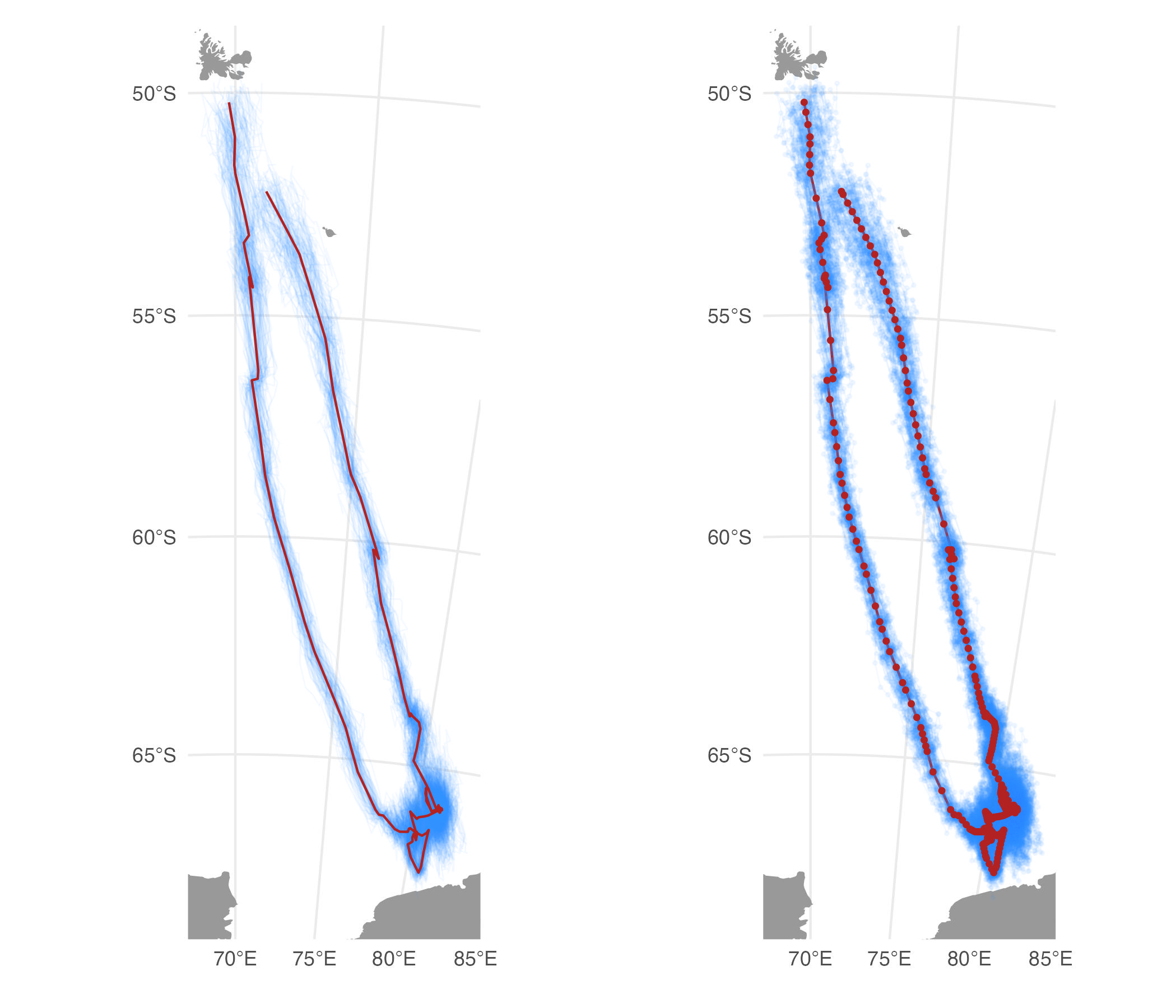

References

Auger-Méthé M, Field C, Albertsen CM, Derocher AE, Lewis MA, Jonsen ID, Mills Flemming J (2016) State-space models’ dirty little secrets: even simple linear Gaussian models can have estimation problems. Scientific reports. 6(1):1-10.

Brillinger DR, Preisler HK, Ager AA, Kie J (2012) The use of potential functions in modelling animal movement. In: Guttorp P., Brillinger D. (eds) Selected Works of David Brillinger. Selected Works in Probability and Statistics. Springer, New York. pp. 385-409.

Hazen et al. (2017) WhaleWatch: a dynamic management tool for predicting blue whale density in the California Current J. Appl. Ecol. 54: 1415-1428.

Hindell MA, Reisinger RR, Ropert-Coudert Y, et al. (2020) Tracking of marine predators to protect Southern Ocean ecosystems. Nature. 580:87–92.